Resonance in AC circuits implies a special frequency determined by the values of the resistance , capacitance , and inductance . For series resonance the condition of resonance is straightforward and it is characterized by minimum impedance and zero phase. Parallel resonance , which is more common in electronic practice, requires a more careful definition.This is an active graphic. Click on either for more detail.

Series Resonance

The resonance of a series RLC circuit occurs when the inductive and capacitive reactances are equal in magnitude but cancel each other because they are 180 degrees apart in phase. The sharp

minimum in impedance which occurs is useful in tuning applications. The sharpness of the minimum depends on the value of R and is characterized by the “Q” of the circuit.

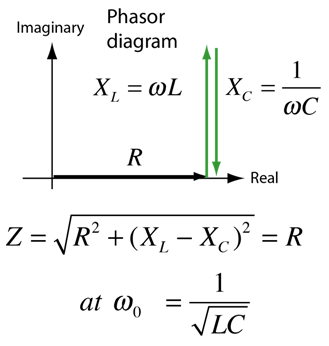Since the current flowing through a series resonance circuit is the product of voltage divided by impedance, at resonance the impedance, Z is at its minimum value, ( =R ). Therefore, the circuit current at this frequency will be at its maximum value of V/R as shown below.

As a series resonance circuit only functions on resonant frequency, this type of circuit is also known as an Acceptor Circuit because at resonance, the impedance of the circuit is at its minimum so easily accepts the current whose frequency is equal to its resonant frequency.
Phase Angle of a Series Resonance Circuit

Parallel Resonance

Let us define what we already know about parallel RLC circuits.

The resonance of a parallel RLC circuit is a bit more involved than the series resonance. The resonant frequency can be defined in three different ways, which converge on the same expression as the series resonant frequency if the resistance of the circuit is small.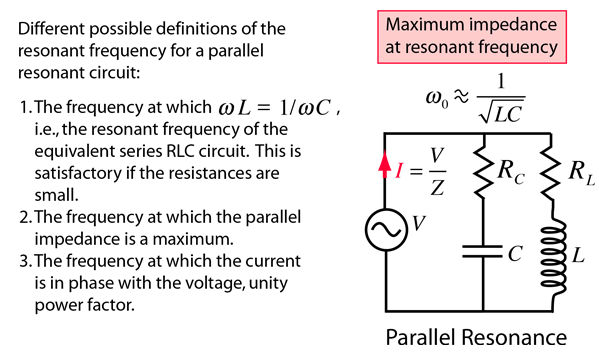

A parallel resonant circuit stores the circuit energy in the magnetic field of the inductor and the electric field of the capacitor. This energy is constantly being transferred back and forth between the inductor and the capacitor which results in zero current and energy being drawn from the supply.

This is because the corresponding instantaneous values of I_L and I_C will always be equal and opposite and therefore the current drawn from the supply is the vector addition of these two currents and the current flowing in I_R.

Also at resonance the parallel LC tank circuit acts like an open circuit with the circuit current being determined by the resistor, R only. So the total impedance of a parallel resonance circuit at resonance becomes just the value of the resistance in the circuit and  Z = R as shown.

Z=(Xc*Xl)/(Xl-Xc) = infinity when Xl=Xc so it is kind of open

resonances circuits