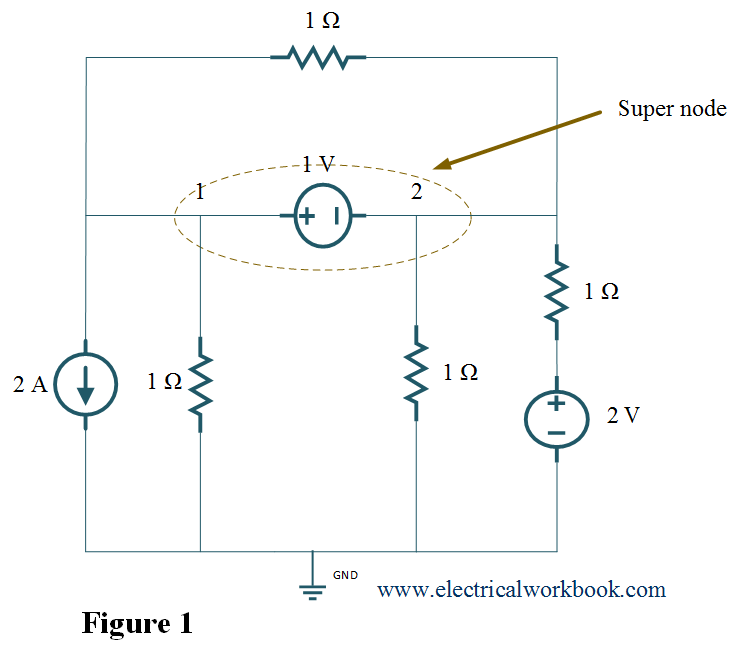
The two nonreference nodes form supernode if the voltage source (dependent or independent) is connected between two nonreference nodes. As shown below in Figure 1, 1 V voltage source is connected between nodes 1 and 2, so node 1 and node 2 forms supernode.
Procedure (steps) for applying Nodal Analysis: –
- Identify the total number of nodes.
- One node selected as reference node and it is assigned to have ground (zero) potential and the remaining nodes called as nonreference node and we assign voltage designations to nonreference nodes. And at last check for supernode.
- Develop the KCL equations for each nonreference node.
- Solve the equations to find the unknown node voltages.
Note:- Apply both KCL and KVL to determine the node voltages.
Example
Example 1. For the given network, find nodal voltages V1 and V2.

Solution:
As shown in the above Figure, given in the question, 1 V voltage source is connected between nodes 1 and 2, so node 1 and node 2 forms supernode. Thus this problem is based on supernode.
Step 1: – The total number of nodes is 3.
Step 2: – Node 0 is selected as reference node and it is assigned to have ground (zero) potential. The remaining node 1 and node 2 are considered as non-reference node shown in Figure 1. Here, node 1 and node 2 forms supernode.
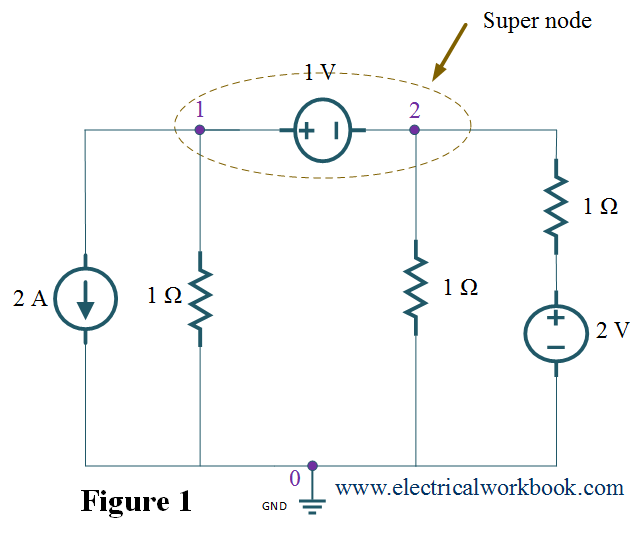
Step 3 and Step 4: – Apply both KCL and KVL to determine the node voltages.
Apply KCL to supernode as shown in Figure 2,
2+(V1–0)/1+(V2–0)/1+(V2–2)/1=0
V1+2V2=0 ……(1)
Apply KVL to the loop having current I as shown in Figure 2,
V1–V2=1 ……(2)
Put Eq.(2) in Eq.(1), we get
3V2+1=0
V2=–1/3 V
From Eq.(1), V1+2V2=0
V1+2(–1/3)=0
V1=2/3 V.


