Common Parts of Conic Sections
A focus is a point about which the conic section is constructed. In other words, it is a point about which rays reflected from the curve converge. A parabola has one focus about which the shape is constructed; an ellipse and hyperbola have two.
A directrix is a line used to construct and define a conic section. The distance of a directrix from a point on the conic section has a constant ratio to the distance from that point to the focus. As with the focus, a parabola has one directrix, while ellipses and hyperbolas have two.

Eccentricity
- 0 < eccentricity < 1 we get an ellipse,
- eccentricity = 1 a parabola, and
- eccentricity > 1 a hyperbola.
A circle has an eccentricity of zero, so the eccentricity shows us how “un-circular” the curve is. The bigger the eccentricity, the less curved it is.
Porabolla
A parabola is a curve where any point is at an equal distance from:
- a fixed point (the focus ), and
- a fixed straight line (the directrix )


Ellipse
“F” is a focus, “G” is a focus,and together they are called foci (pronounced “fo-sigh”).
The total distance from F to P to G stays the same
Well f+g is equal to the length of the major axis.


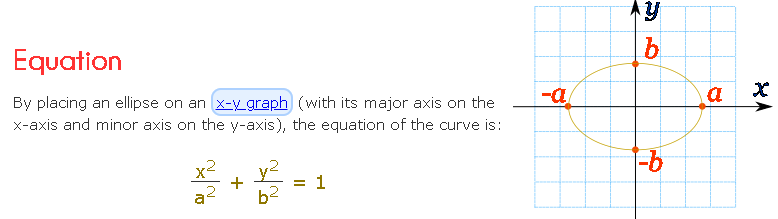

Hyperbola
A hyperbola is two curves that are like infinite bows.
Looking at just one of the curves:
any point P is closer to F than to G by some constant amount
The other curve is a mirror image, and is closer to G than to F.

- an axis of symmetry (that goes through each focus)
- two vertices (where each curve makes its sharpest turn)
- the distance between the vertices (2a on the diagram) is the constant difference between the lengths PF and PG
- two asymptotes which are not part of the hyperbola but show where the curve would go if continued indefinitely in each of the four directions


Hyperbolic functions




Catenary (hanging cable)



