Zener
Voltage Vz: The Zener voltage or reverse voltage specification of the diode is often designated by the letters Vz.
Current : The current, IZM, of a Zener diode is the maximum current that can flow through a Zener diode at its rated voltage, VZ.
Typically there is also a minimum current required for the operation of the diode. As a rough rule of thumb, this can be around 5 to 10 mA for a typical leaded 400 mW device. Below this current level, the diode does not break down adequately to maintain its stated voltage.
It is best to keep the Zener diode running above this minimum value with some margin, but without the likelihood of it dissipating too much power when the Zener needs to pass more current.
Power rating: All Zener diodes have a power rating that should not be exceeded. This defines the maximum power that can be dissipated by the package, and it is the product of the voltage across the diode multiplied by the current flowing through it.
Zener resistance Rz: The IV characteristic of the Zener diode is not completely vertical in the breakdown region. This means that for slight changes in current, there will be a small change in the voltage across the diode. The voltage change for a given change in current is the resistance of the diode. This value of resistance, often termed the resistance is designated Rz.

The inverse of the slope shown is referred to as the dynamic resistance of the diode, and this parameter is often noted in the manufacturers’ datasheets. Typically the slope does not vary much for different current levels, provided they are between about 0.1 and 1 times the rated current Izt.

Voltage tolerance: With diodes being marked and sorted to meet the E12 or E24 value ranges, typical tolerance specifications for the diode are ±5%. Some datasheets may specify the voltage as a typical voltage and then provide a maximum and minimum.
How to use a Zener Diode
As said a Zener diode will mostly be used in a protection circuit or in a crude voltage regulator circuit. Either way, it very important to remember that a Zener diode should always be used along with a Zener resistor.
A Zener resistor is nothing but an ordinary resistor which is used for current limiting purpose. This resistor decides (limits) the amount of current that can flow through the Zener diode or through the load connected to Zener diode; this was the Zener diode is protected from high current. If this resistor is not used the diode will be damaged due to high current. A simple Zener diode circuit is shown below.
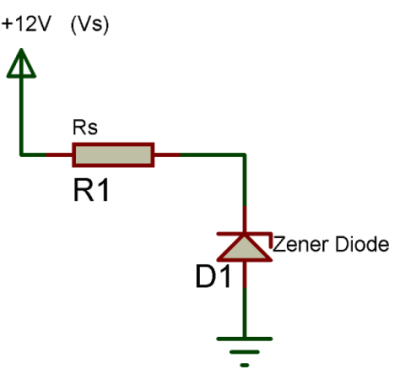
In the above circuit the formulae to calculate the Zener series resistor Rs is shown below
Rs = (Vs – Vz) / Iz
For a 1N4732A Zener diode the value of Vz is 4.7V and Pz is 500mW as mentioned in specifications above, now with supply voltage (Vs) of 12V the value of Rs will be
Rs = (12-4.7)/Iz Iz = Pz/Vz = 500mW / 4.7V = ~106mA Therefore, Rs = (12-4.7)/106 = 68 ohms Rs = 68ohms (approx)
Diode
Semiconductor material:
Silicon: The forward turn on voltage is around 0.6V, which is high for some applications, although for Schottky diodes it is less.
Germanium: Germanium is less widely used and but offers a low turn on voltage of around 0.2 to 0.3 V.
Diode type: Zener diodes are used for providing reference voltages, whilst varactor diodes are used to provide a variable level of capacitance in an RF design according to the reverse bias provided. Rectifier diodes may use a straightforward PN junction diode, or in some cases they may use a Schottky diode for a lower forward voltage. Whatever the application is is necessary to use the right type of diode to obtain the required functionality and performance.
Forward voltage drop, Vf: Any electronics device passing current will develop a resulting voltage across it and this diode characteristic is of great importance, especially for power rectification where power losses will be higher for a high forward voltage drop. Also diodes for RF designs often need a small forward voltage drop as signals may be small but still need to overcome it.
Reverse breakdown voltage, V(BR)R: This is a little different to the peak inverse voltage in that this voltage is the point at which the diode will break down.
Maximum forward current If: For an electronic circuit design that passes any levels of current it is necessary to ensure that the maximum current levels for the diode are not exceeded. As the current levels rise, so additional heat is dissipated and this needs to be removed.
Leakage current Ir: If a perfect diode were available, then no current would flow when it was reverse biased. It is found that for a real PN junction diode, a very small amount of current flow in the reverse direction as a result of the minority carriers in the semiconductor. The level of leakage current is dependent upon three main factors. The reverse voltage is obviously significant. It is also temperature dependent, rising appreciably with temperature. It is also found that it is very dependent upon the type of semiconductor material used – silicon is very much better than germanium.

The leakage current characteristic or specification for a PN junction diode is specified at a certain reverse voltage and particular temperature. The specification is normally defined in terms of in microamps, µA or picoamps, pA as the levels are normally very low before reverse breakdown occurs.
| CHARACTERISTIC | TYPICAL VALUE | UNIT | DETAILS |
|---|---|---|---|
| Max DC Blocking Voltage, Vr | 70 | V | |
| Max forward continuous current, Ifm | 15 | mA | |
| Reverse breakdown voltage, V(BR)R | 70 | V | @ reverse current of 10µA |
| Reverse leakage current, IR | 200 | µA | At VR=50V |
| Forward voltage drop, VF | 0.41 1.00 | V | at IF = 1.0 mA IF=15mA |
| Junction capacitance, Cj | 2.0 | pF | VR = 0V, f=1MHz |
| Reverse recovery time, trr | 1 | nS |