data structure – MAlabdali

Tree Traversals

by malabdaliAugust 8, 2021August 8, 2021data structure

Depth-First Search and Breadth-First Search

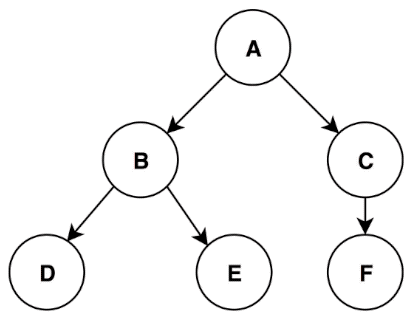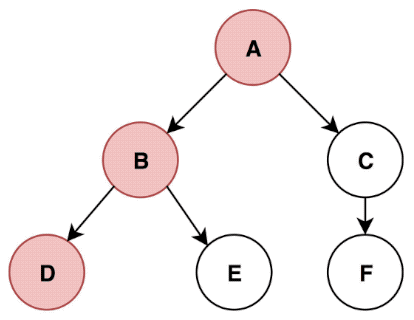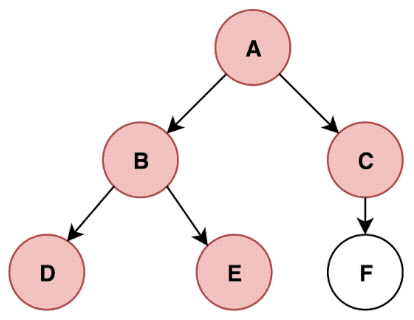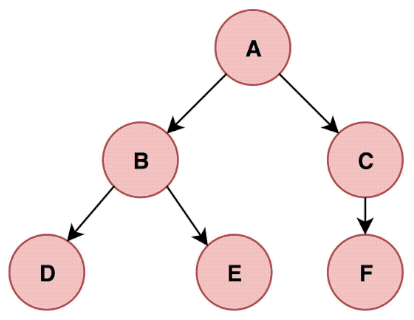
class Node{
    int value;
    Node *parent;
    std::vector<Node*> childs;
public:
    Node(int v):value(v){

    }
    void AppendChild(Node* n){
        n->parent=this;
        childs.push_back(n);
    }
    void RemoveChild(Node* n){
        n->parent=nullptr;
        this->childs.erase(std::find(childs.begin(),childs.end(),n));
    }
    void AppendChilds(std::initializer_list<Node*> childs){
        for(Node* n:childs)
            this->AppendChild(n);
    }
    std::vector<Node*> GetChildren(){
        return childs;
    }
    Node* GetParent(){
        return parent;
    }
    Node* GetRoot(){
        Node* root=this;
        while(root->GetParent())
            root=parent->GetParent();
        return root;
    }
    operator int(){
        return value;
    }
};

void DFS(Node* root){
    qDebug()<<*root;
    std::vector<Node*> nodes=root->GetChildren();
    for(Node* n:nodes)
        DFS(n);
}

void BFS(Node* root){
    std::queue<Node*> nodes;
    nodes.push(root);
    while(nodes.size()>0){
        Node* current=nodes.front();
        nodes.pop();
        qDebug()<<*current;
        for(Node* n : current->GetChildren())
            nodes.push(n);
    }
}

int main(int argc, char *argv[])
{
    QGuiApplication a(argc, argv);
    Node n1=1,n2=2,n3=3,n4=4,n5=5,n6=6,n7=7,n8=8,n9=9,n10=10,n11=11,n12=12,n13=13,n14=14,n15=15,n16=16,n17=17,n18=18,n19=19;
    n1.AppendChilds({&n2,&n3});
    n2.AppendChilds({&n4,&n5});
    n3.AppendChilds({&n6,&n7});
    n4.AppendChilds({&n8,&n9});
    n5.AppendChilds({&n10,&n11});
    n6.AppendChilds({&n12,&n13});
    n7.AppendChilds({&n14,&n15});
    n8.AppendChilds({&n16,&n17});
    n9.AppendChilds({&n18,&n19});
    BFS(&n1);

    return a.exec();
}

Binary Tree Traversals

struct Node {
    int data;
    struct Node *left, *right;
    Node(int data)
    {
        this->data = data;
        left = right = NULL;
    }
};
 
/* Given a binary tree, print its nodes according to the
"bottom-up" postorder traversal. */
void printPostorder(struct Node* node)
{
    if (node == NULL)
        return;
 
    // first recur on left subtree
    printPostorder(node->left);
 
    // then recur on right subtree
    printPostorder(node->right);
 
    // now deal with the node
    cout << node->data << " ";
}
 
/* Given a binary tree, print its nodes in inorder*/
void printInorder(struct Node* node)
{
    if (node == NULL)
        return;
 
    /* first recur on left child */
    printInorder(node->left);
 
    /* then print the data of node */
    cout << node->data << " ";
 
    /* now recur on right child */
    printInorder(node->right);
}
 
/* Given a binary tree, print its nodes in preorder*/
void printPreorder(struct Node* node)
{
    if (node == NULL)
        return;
 
    /* first print data of node */
    cout << node->data << " ";
 
    /* then recur on left sutree */
    printPreorder(node->left);
 
    /* now recur on right subtree */
    printPreorder(node->right);
}
 
/* Driver program to test above functions*/
int main()
{
    struct Node* root = new Node(1);
    root->left = new Node(2);
    root->right = new Node(3);
    root->left->left = new Node(4);
    root->left->right = new Node(5);
 
    cout << "\nPreorder traversal of binary tree is \n";
    printPreorder(root);
 
    cout << "\nInorder traversal of binary tree is \n";
    printInorder(root);
 
    cout << "\nPostorder traversal of binary tree is \n";
    printPostorder(root);
 
    return 0;
}

Arithmetic Expression Tree

after that we can calculate the tree by postfix or post-order

Sorting Algorithms

by malabdaliAugust 8, 2021data structure / programming

it is sometimes useful to know if a sorting algorithm is stable
A sorting algorithm is stable if it preserves the original order of elements with equal key values (where the key is the value the algorithm sorts by). For example,

Bubble Sort

Bubble Sort is the simplest sorting algorithm that works by repeatedly swapping the adjacent elements if they are in wrong order.
Example:


First Pass: 
( 5 1 4 2 8 ) –> ( 1 5 4 2 8 ), Here, algorithm compares the first two elements, and swaps since 5 > 1. 
( 1 5 4 2 8 ) –>  ( 1 4 5 2 8 ), Swap since 5 > 4 
( 1 4 5 2 8 ) –>  ( 1 4 2 5 8 ), Swap since 5 > 2 
( 1 4 2 5 8 ) –> ( 1 4 2 5 8 ), Now, since these elements are already in order (8 > 5), algorithm does not swap them.
Second Pass: 
( 1 4 2 5 8 ) –> ( 1 4 2 5 8 ) 
( 1 4 2 5 8 ) –> ( 1 2 4 5 8 ), Swap since 4 > 2 
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 ) 
( 1 2 4 5 8 ) –>  ( 1 2 4 5 8 ) 
Now, the array is already sorted, but our algorithm does not know if it is completed. The algorithm needs one whole pass without any swap to know it is sorted.
Third Pass: 
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 ) 
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 ) 
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 ) 
( 1 2 4 5 8 ) –> ( 1 2 4 5 8 )

template<class T>
void Swap(T* p1,T* p2){
    T p3=*p1;
    *p1=*p2;
    *p2=p3;
    return;
}

template<typename T ,int size>
void BubbleSort(T (&t)[size]){
    for(int i=1;i<size;i++){
        for(int ii=0;ii<size-i;ii++){
            if(t[ii]>t[ii+1])
                Swap(t+(ii+1),t+(ii));
        }
    }
}

Insertion Sort

void insertionSort(int arr[], int n)
{
    int i, key, j;
    for (i = 1; i < n; i++)
    {
        key = arr[i];
        j = i - 1;
        while (j >= 0 && arr[j] > key)
        {
            arr[j + 1] = arr[j];
            j = j - 1;
        }
        arr[j + 1] = key;
    }
}

Merge Sort

void merge(int array[], int const left, int const mid, int const right)
{
    auto const subArrayOne = mid - left + 1;
    auto const subArrayTwo = right - mid;

    auto *leftArray = new int[subArrayOne],
         *rightArray = new int[subArrayTwo];

    for (auto i = 0; i < subArrayOne; i++)
        leftArray[i] = array[left + i];
    for (auto j = 0; j < subArrayTwo; j++)
        rightArray[j] = array[mid + 1 + j];
 
    auto indexOfSubArrayOne = 0, 
        indexOfSubArrayTwo = 0; 
    int indexOfMergedArray = left; 
 
    while (indexOfSubArrayOne < subArrayOne && indexOfSubArrayTwo < subArrayTwo) {
        if (leftArray[indexOfSubArrayOne] <= rightArray[indexOfSubArrayTwo]) {
            array[indexOfMergedArray] = leftArray[indexOfSubArrayOne];
            indexOfSubArrayOne++;
        }
        else {
            array[indexOfMergedArray] = rightArray[indexOfSubArrayTwo];
            indexOfSubArrayTwo++;
        }
        indexOfMergedArray++;
    }

    while (indexOfSubArrayOne < subArrayOne) {
        array[indexOfMergedArray] = leftArray[indexOfSubArrayOne];
        indexOfSubArrayOne++;
        indexOfMergedArray++;
    }

    while (indexOfSubArrayTwo < subArrayTwo) {
        array[indexOfMergedArray] = rightArray[indexOfSubArrayTwo];
        indexOfSubArrayTwo++;
        indexOfMergedArray++;
    }
}

void mergeSort(int array[], int const begin, int const end)
{
    if (begin >= end)
        return; 
    auto mid = begin + (end - begin) / 2;
    mergeSort(array, begin, mid);
    mergeSort(array, mid + 1, end);
    merge(array, begin, mid, end);
}

Quick Sort

The key process in quickSort is partition(). Target of partitions is, given an array and an element x of array as pivot, put x at its correct position in sorted array and put all smaller elements (smaller than x) before x, and put all greater elements (greater than x) after x. All this should be done in linear time.

#include <bits/stdc++.h>
using namespace std;

void swap(int* a, int* b)
{
    int t = *a;
    *a = *b;
    *b = t;
}

int partition (int arr[], int low, int high)
{
    int pivot = arr[high]; // pivot
    int i = (low - 1); // Index of smaller element and indicates the right position of pivot found so far
 
    for (int j = low; j <= high - 1; j++)
    {
        if (arr[j] < pivot)
        {
            i++;
            swap(&arr[i], &arr[j]);
        }
    }
    swap(&arr[i + 1], &arr[high]);
    return (i + 1);
}

void quickSort(int arr[], int low, int high)
{
    if (low < high)
    {
        int pi = partition(arr, low, high);
        quickSort(arr, low, pi - 1);
        quickSort(arr, pi + 1, high);
    }
}

Counting Sort

void countSort(char arr[])
{
    char output[strlen(arr)];
    int count[RANGE + 1], i;
    memset(count, 0, sizeof(count));
    for (i = 0; arr[i]; ++i)
        ++count[arr[i]];
    for (i = 1; i <= RANGE; ++i)
        count[i] += count[i - 1];
    for (i = 0; arr[i]; ++i) {
        output[count[arr[i]] - 1] = arr[i];
        --count[arr[i]];
    }
    for (i = 0; arr[i]; ++i)
        arr[i] = output[i];
}

void countSort(vector<int>& arr)
{
    int max = *max_element(arr.begin(), arr.end());
    int min = *min_element(arr.begin(), arr.end());
    int range = max - min + 1;
 
    vector<int> count(range), output(arr.size());
    for (int i = 0; i < arr.size(); i++)
        count[arr[i] - min]++;
 
    for (int i = 1; i < count.size(); i++)
        count[i] += count[i - 1];
 
    for (int i = arr.size() - 1; i >= 0; i--) {
        output[count[arr[i] - min] - 1] = arr[i];
        count[arr[i] - min]--;
    }
 
    for (int i = 0; i < arr.size(); i++)
        arr[i] = output[i];
}

binary heap

by malabdaliJuly 17, 2020c++ / data structure

A binary heap is a heap data structure that takes the form of a binary tree. Binary heaps are a common way of implementing priority queues.^[1]^:162–163 The binary heap was introduced by J. W. J. Williams in 1964, as a data structure for heapsort.^[2]

A binary heap is defined as a binary tree with two additional constraints:^[3]

Shape property: a binary heap is a complete binary tree; that is, all levels of the tree, except possibly the last one (deepest) are fully filled, and, if the last level of the tree is not complete, the nodes of that level are filled from left to right.
Heap property: the key stored in each node is either greater than or equal to (≥) or less than or equal to (≤) the keys in the node’s children, according to some total order.

Heaps where the parent key is greater than or equal to (≥) the child keys are called max-heaps; those where it is less than or equal to (≤) are called min-heaps. Efficient (logarithmic time) algorithms are known for the two operations needed to implement a priority queue on a binary heap: inserting an element, and removing the smallest or largest element from a min-heap or max-heap, respectively. Binary heaps are also commonly employed in the heapsort sorting algorithm, which is an in-place algorithm because binary heaps can be implemented as an implicit data structure, storing keys in an array and using their relative positions within that array to represent child-parent relationships.

insert

Add the element to the bottom level of the heap at the most left.
Compare the added element with its parent; if they are in the correct order, stop.
If not, swap the element with its parent and return to the previous step.

This image has an empty alt attribute; its file name is 2-18.png — Insert “15”

This image has an empty alt attribute; its file name is 3-10.png — Insert “15”

Remove

Replace the root of the heap with the last element on the last level.
Compare the new root with its children; if they are in the correct order, stop.
If not, swap the element with one of its children and return to the previous step. (Swap with its smaller child in a min-heap and its larger child in a max-heap.)

This image has an empty alt attribute; its file name is 5-3.png — extract “11”

This image has an empty alt attribute; its file name is 6-3.png — extract “11”

Heap in C++

You can create with std::make_heap a heap. You can push with std::push_heap new elements on the heap. On the contrary, you can pop the largest element with std::pop_heap from the heap. Both operations respect the heap characteristics. std::push_heap moves the last element of the range on the heap; std::pop_heap moves the biggest element of the heap to the last position in the range. You can check with std::is_heap if a range is a heap. You can determine with std::is_heap_until until which position the range is a heap. std::sort_heap sorts the heap.

std::vector<int> vec{4, 3, 2, 1, 5, 6, 7, 9, 10};
std::make_heap(vec.begin(), vec.end());
for (auto v: vec) std::cout << v << " ";                   // 10 9 7 4 5 6 2 3 1
std::cout << std::is_heap(vec.begin(), vec.end());         // true

vec.push_back(100);
std::cout << std::is_heap(vec.begin(), vec.end());         // false
std::cout << *std::is_heap_until(vec.begin(), vec.end());  // 100
for (auto v: vec) std::cout << v << " ";                   // 10 9 7 4 5 6 2 3 1 100

std::push_heap(vec.begin(), vec.end());
std::cout << std::is_heap(vec.begin(), vec.end());        // true
for (auto v: vec) std::cout << v << " ";                  // 100 10 7 4 9 6 2 3 1 5

std::pop_heap(vec.begin(), vec.end());
for (auto v: vec) std::cout << v << " ";                  // 10 9 7 4 5 6 2 3 1 100
std::cout << *std::is_heap_until(vec.begin(), vec.end()); // 100

vec.resize(vec.size()-1);
std::cout << std::is_heap(vec.begin(), vec.end());        // true
std::cout << vec.front() << std::endl;                    // 10