Millman theorem

by malabdalicircuit analysis

In Millman’s Theorem, the circuit is re-drawn as a parallel network of branches, each branch containing a resistor or series battery/resistor combination. Millman’s Theorem is applicable only to those circuits which can be redrawn accordingly. Here again, is our example circuit used for the last two analysis methods:

parallel network branches circuit

And here is that same circuit, re-drawn for the sake of applying Millman’s Theorem:

parallel network branches circuit

By considering the supply voltage within each branch and the resistance within each branch, Millman’s Theorem will tell us the voltage across all branches. Please note that I’ve labeled the battery in the rightmost branch as “B3” to clearly denote it as being in the third branch, even though there is no “B2” in the circuit!

Millman’s Theorem Equation

Millman’s Theorem is nothing more than a long equation, applied to any circuit drawn as a set of parallel-connected branches, each branch with its own voltage source and series resistance:

millmans theorem equation

Substituting actual voltage and resistance figures from our example circuit for the variable terms of this equation, we get the following expression:

millmans theorem equation actual value

The final answer of 8 volts is the voltage seen across all parallel branches, like this:

voltage across parallel branches

The polarity of all voltages in Millman’s Theorem is referenced to the same point. In the example circuit above, I used the bottom wire of the parallel circuit as my reference point, and so the voltages within each branch (28 for the R1 branch, 0 for the R2 branch, and 7 for the R3 branch) were inserted into the equation as positive numbers. Likewise, when the answer came out to 8 volts (positive), this meant that the top wire of the circuit was positive with respect to the bottom wire (the original point of reference). If both batteries had been connected backward (negative end up and positive ends down), the voltage for branch 1 would have been entered into the equation as -28 volts, the voltage for branch 3 as -7 volts, and the resulting answer of -8 volts would have told us that the top wire was negative with respect to the bottom wire (our initial point of reference).

Solving for Resistor Voltage Drops

To solve for resistor voltage drops, the Millman voltage (across the parallel network) must be compared against the voltage source within each branch, using the principle of voltages adding in series to determine the magnitude and polarity of the voltage across each resistor:

equation for resistor voltage drops

Solving for Branch Currents

To solve for branch currents, each resistor voltage drop can be divided by its respective resistance (I=E/R):

solving for branch currents

Determining the Direction of Current

The direction of current through each resistor is determined by the polarity across each resistor, not by the polarity across each battery, as the current can be forced back through a battery, as is the case with B3 in the example circuit. This is important to keep in mind since Millman’s Theorem doesn’t provide as direct an indication of “wrong” current direction as does the Branch Current or Mesh Current methods. You must pay close attention to the polarities of resistor voltage drops as given by Kirchhoff’s Voltage Law, determining the direction of currents from that.

determining the direction of current

Millman’s Theorem is very convenient for determining the voltage across a set of parallel branches, where there are enough voltage sources present to preclude solution via regular series-parallel reduction method. It also is easy in the sense that it doesn’t require the use of simultaneous equations. However, it is limited in that it only applied to circuits which can be re-drawn to fit this form. It cannot be used, for example, to solve an unbalanced bridge circuit. And, even in cases where Millman’s Theorem can be applied, the solution of individual resistor voltage drops can be a bit daunting to some, the Millman’s Theorem equation only providing a single figure for branch voltage.

As you will see, each network analysis method has its own advantages and disadvantages. Each method is a tool, and there is no tool that is perfect for all jobs. The skilled technician, however, carries these methods in his or her mind like a mechanic carries a set of tools in his or her toolbox. The more tools you have equipped yourself with, the better prepared you will be for any eventuality.

proof

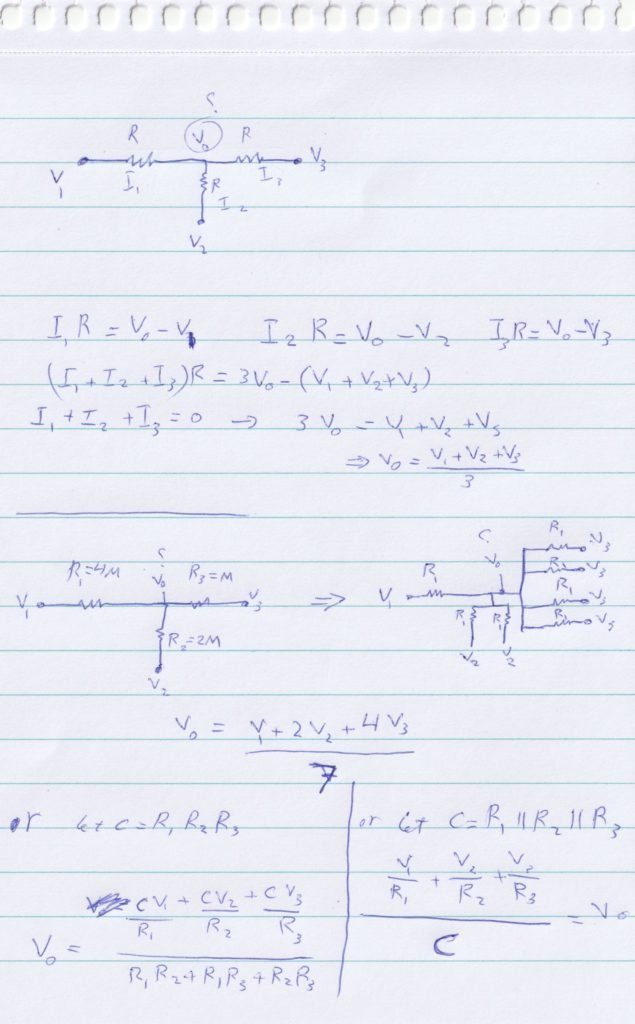
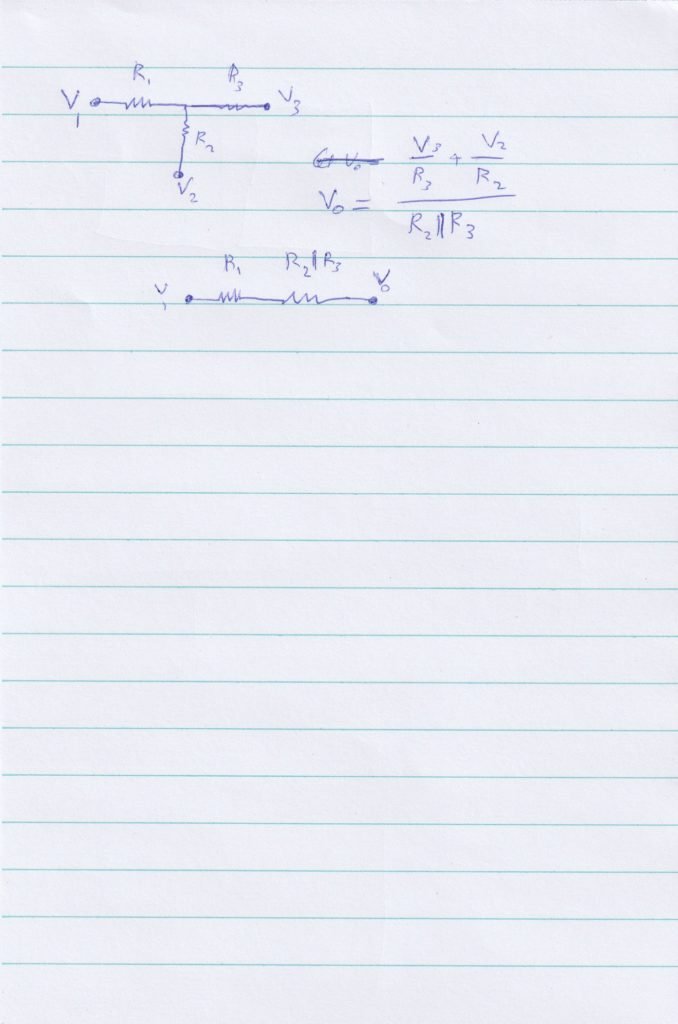
note change C to

r1||r2||r3 -> \frac{1}{(r1||r2||r3)}
r1||r2 -> \frac{1}{(r1||r2)}

10,555 thoughts on “Millman theorem”

  167. Hey There. I found your blog using msn. This is a very
    well written article. I will make sure to bookmark it and come back to read
    more of your useful info. Thanks for the post. I’ll certainly
    comeback.

  284. Let me give you a thumbs up man. Can I show my hidden information on amazing values and if you want to have a checkout and
    also share valuable info about how to become a millionaire
    yalla lready know follow me my fellow commenters!.

  295. Я ценю балансировку автора в описании проблемы. Он предлагает читателю достаточно аргументов и контекста для формирования собственного мнения, не внушая определенную точку зрения.

  304. Надеюсь, что эти комментарии добавят ещё больше положительных настроений к информационной статье!

  320. We’re a group of volunteers and opening a new scheme in our community.
    Your web site provided us with valuable info to work on.
    You’ve done an impressive job and our entire community will be thankful to
    you.

  405. magnificent post, very informative. I wonder why the other specialists of this sector do not notice this. You should continue your writing. I am sure, you have a great readers’ base already!

  437. Thanks for the good writeup. It if truth be told
    was a entertainment account it. Look advanced to far introduced agreeable from you!
    By the way, how can we keep in touch?

  574. The other day, while I was at work, my cousin stole my apple ipad and tested to see if it can survive a thirty foot drop, just so she can be a youtube sensation.
    My apple ipad is now broken and she has 83 views. I know this is entirely off topic but I had to
    share it with someone!

  609. Очень хорошо структурированная статья! Я оцениваю ясность и последовательность изложения. Благодаря этому, я смог легко следовать за логикой и усвоить представленную информацию. Большое спасибо автору за такой удобный формат!

  618. After looking at a handful of the blog posts on your web site,
    I seriously appreciate your way of blogging. I book marked it to my
    bookmark website list and will be checking back in the near future.
    Take a look at my web site too and let me know what you think.

  636. Whats up very cool website!! Guy .. Beautiful .. Superb .. I’ll bookmark your blog and take the feeds also?KI am satisfied to seek out a lot of useful information here in the put up, we want work out more techniques in this regard, thanks for sharing. . . . . .

  663. Hi there it’s me, I am also visiting this website regularly,
    this site is really pleasant and the users are genuinely
    sharing fastidious thoughts.

  699. Я просто не могу пройти мимо этой статьи без оставления положительного комментария. Она является настоящим примером качественной журналистики и глубокого исследования. Очень впечатляюще!