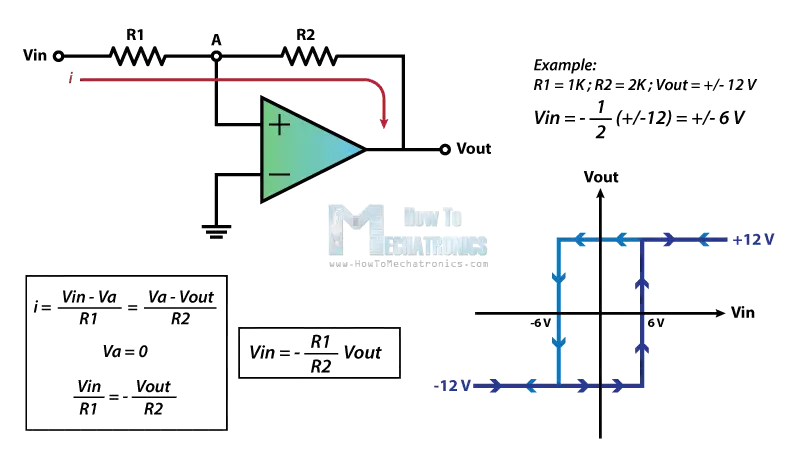
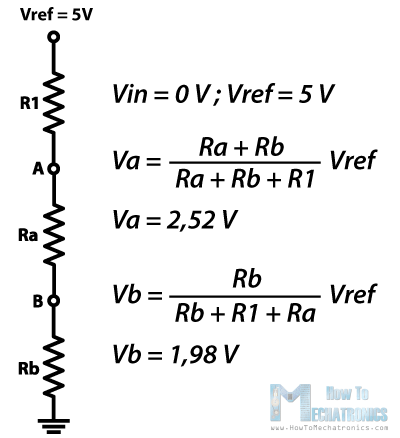
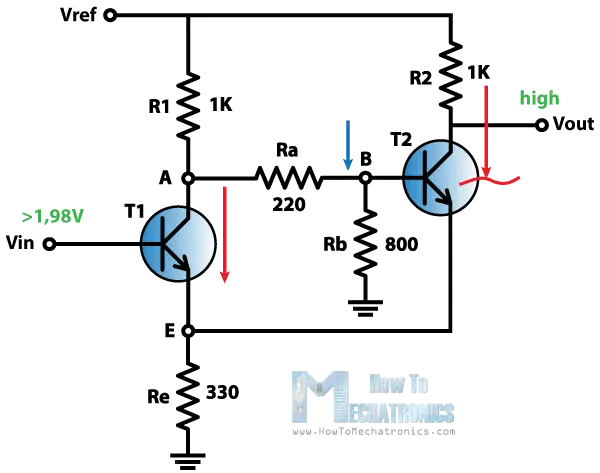
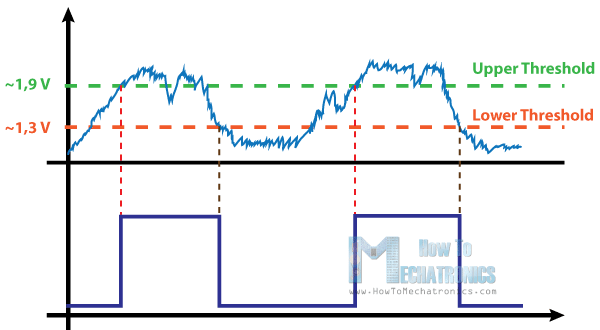
Regenerative switching circuits such as Astable Multivibrators are the most commonly used type of relaxation oscillator because not only are they simple, reliable and ease of construction they also produce a constant square wave output waveform.

Unlike the Monostable Multivibrator or the Bistable Multivibrator we looked at in the previous tutorials that require an “external” trigger pulse for their operation, the Astable Multivibrator has automatic built in triggering which switches it continuously between its two unstable states both set and reset.

The Astable Multivibrator is another type of cross-coupled transistor switching circuit that has NO stable output states as it changes from one state to the other all the time. The astable circuit consists of two switching transistors, a cross-coupled feedback network, and two time delay capacitors which allows oscillation between the two states with no external triggering to produce the change in state.

In electronic circuits, astable multivibrators are also known as Free-running Multivibrator as they do not require any additional inputs or external assistance to oscillate. Astable oscillators produce a continuous square wave from its output or outputs, (two outputs no inputs) which can then be used to flash lights or produce a sound in a loudspeaker.

The basic transistor circuit for an Astable Multivibrator produces a square wave output from a pair of grounded emitter cross-coupled transistors. Both transistors either NPN or PNP, in the multivibrator are biased for linear operation and are operated as Common Emitter Amplifiers with 100% positive feedback.

This configuration satisfies the condition for oscillation when: ( βA = 1∠ 0^o ). This results in one stage conducting “fully-ON” (Saturation) while the other is switched “fully-OFF” (cut-off) giving a very high level of mutual amplification between the two transistors. Conduction is transferred from one stage to the other by the discharging action of a capacitor through a resistor as shown below.

Basic Astable Multivibrator Circuit

Assume a 6 volt supply and that transistor, TR₁ has just switched “OFF” (cut-off) and its collector voltage is rising towards Vcc, meanwhile transistor TR₂ has just turned “ON”. Plate “A” of capacitor C1 is also rising towards the +6 volts supply rail of Vcc as it is connected to the collector of TR₁ which is now cut-off. Since TR₁ is in cut-off, it conducts no current so there is no volt drop across load resistor R₁.

The other side of capacitor, C1, plate “B”, is connected to the base terminal of transistor TR₂ and at 0.6v because transistor TR₂ is conducting (saturation). Therefore, capacitor C1 has a potential difference of +5.4 volts across its plates, (6.0 – 0.6v) from point A to point B.

Since TR₂ is fully-on, capacitor C₂ starts to charge up through resistor R₂ towards Vcc. When the voltage across capacitor C₂ rises to more than 0.6v, it biases transistor TR₁ into conduction and into saturation.

The instant that transistor, TR₁ switches “ON”, plate “A” of the capacitor which was originally at Vcc potential, immediately falls to 0.6 volts. This rapid fall of voltage on plate “A” causes an equal and instantaneous fall in voltage on plate “B” therefore plate “B” of C1 is pulled down to -5.4v (a reverse charge) and this negative voltage swing is applied the base of TR₂ turning it hard “OFF”. One unstable state.

Transistor TR₂ is driven into cut-off so capacitor C1 now begins to charge in the opposite direction via resistor R3 which is also connected to the +6 volts supply rail, Vcc. Thus the base of transistor TR₂ is now moving upwards in a positive direction towards Vcc with a time constant equal to the C1 x R3 combination.

However, it never reaches the value of Vcc because as soon as it gets to 0.6 volts positive, transistor TR₂ turns fully “ON” into saturation. This action starts the whole process over again but now with capacitor C2 taking the base of transistor TR₁ to -5.4v while charging up via resistor R2 and entering the second unstable state.

Then we can see that the circuit alternates between one unstable state in which transistor TR₁ is “OFF” and transistor TR₂ is “ON”, and a second unstable in which TR₁ is “ON” and TR₂ is “OFF” at a rate determined by the RC values. This process will repeat itself over and over again as long as the supply voltage is present.

The amplitude of the output waveform is approximately the same as the supply voltage, Vcc with the time period of each switching state determined by the time constant of the RC networks connected across the base terminals of the transistors. As the transistors are switching both “ON” and “OFF”, the output at either collector will be a square wave with slightly rounded corners because of the current which charges the capacitors. This could be corrected by using more components as we will discuss later.

If the two time constants produced by C2 x R2 and C1 x R3 in the base circuits are the same, the mark-to-space ratio ( t1/t2 ) will be equal to one-to-one making the output waveform symmetrical in shape. By varying the capacitors, C1, C2 or the resistors, R2, R3 the mark-to-space ratio and therefore the frequency can be altered.

We saw in the RC Discharging tutorial that the time taken for the voltage across a capacitor to fall to half the supply voltage, 0.5Vcc is equal to 0.69 time constants of the capacitor and resistor combination. Then taking one side of the astable multivibrator, the length of time that transistor TR₂ is “OFF” will be equal to 0.69T or 0.69 times the time constant of C1 x R3. Likewise, the length of time that transistor TR₁ is “OFF” will be equal to 0.69T or 0.69 times the time constant of C2 x R2 and this is defined as.

Astable Multivibrators Periodic Time

Where, R is in Ω’s and C in Farads.

By altering the time constant of just one RC network the mark-to-space ratio and frequency of the output waveform can be changed but normally by changing both RC time constants together at the same time, the output frequency will be altered keeping the mark-to-space ratios the same at one-to-one.

If the value of the capacitor C1 equals the value of the capacitor, C2, C1 = C2 and also the value of the base resistor R2 equals the value of the base resistor, R3, R2 = R3 then the total length of time of the Multivibrators cycle is given below for a symmetrical output waveform.

Frequency of Oscillation

Where, R is in Ω’s, C is in Farads, T is in seconds and ƒ is in Hertz.

and this is known as the “Pulse Repetition Frequency”. So Astable Multivibrators can produce TWO very short square wave output waveforms from each transistor or a much longer rectangular shaped output either symmetrical or non-symmetrical depending upon the time constant of the RC network as shown below.

Astable Multivibrator Waveforms

Astable Multivibrator Example No1

An Astable Multivibrators circuit is required to produce a series of pulses at a frequency of 500Hz with a mark-to-space ratio of 1:5. If  R2 = R3 = 100kΩ, calculate the values of the capacitors, C1 and C2 required.

and by rearranging the formula above for the periodic time, the values of the capacitors required to give a mark-to-space ratio of 1:5 are given as:

The values of 4.83nF and 24.1nF respectively, are calculated values, so we would need to choose the nearest preferred values for C1 and C2 allowing for the capacitors tolerance. In fact due to the wide range of tolerances associated with the humble capacitor the actual output frequency may differ by as much as ±20%, (400 to 600Hz in our simple example) from the actual frequency needed.

If we require the output astable waveform to be non-symmetrical for use in timing or gating type circuits, etc, we could manually calculate the values of R and C for the individual components required as we did in the example above. However, when the two R’s and C´s are both equal, we can make our life a little bit easier for ourselves by using tables to show the astable multivibrators calculated frequencies for different combinations or values of both R and C. For example,

Astable Multivibrator Frequency Table

Res.	Capacitor Values
1nF	2.2nF	4.7nF	10nF	22nF	47nF	100nF	220nF	470nF
1.0kΩ	714.3kHz	324.6kHz	151.9kHz	71.4kHz	32.5kHz	15.2kHz	7.1kHz	3.2kHz	1.5kHz
2.2kΩ	324.7kHz	147.6kHz	69.1kHz	32.5kHz	14.7kHz	6.9kHz	3.2kHz	1.5kHz	691Hz
4.7kΩ	151.9kHz	69.1kHz	32.3kHz	15.2kHz	6.9kHz	3.2kHz	1.5kHz	691Hz	323Hz
10kΩ	71.4kHz	32.5kHz	15.2kHz	7.1kHz	3.2kHz	1.5kHz	714Hz	325Hz	152Hz
22kΩ	32.5kHz	14.7kHz	6.9kHz	3.2kHz	1.5kHz	691Hz	325Hz	147Hz	69.1Hz
47kΩ	15.2kHz	6.9kHz	3.2kHz	1.5kHz	691Hz	323Hz	152Hz	69.1Hz	32.5Hz
100kΩ	7.1kHz	3.2kHz	1.5kHz	714Hz	325Hz	152Hz	71.4Hz	32.5Hz	15.2Hz
220kΩ	3.2kHz	1.5kHz	691Hz	325Hz	147Hz	69.1Hz	32.5Hz	15.2Hz	6.9Hz
470kΩ	1.5kHz	691Hz	323Hz	152Hz	69.1Hz	32.5Hz	15.2Hz	6.6Hz	3.2Hz
1MΩ	714Hz	325Hz	152Hz	71.4Hz	32.5Hz	15.2Hz	6.9Hz	3.2Hz	1.5Hz

Pre-calculated frequency tables can be very useful in determining the required values of both R and C for a particular symmetrical output frequency without the need to keep recalculating them every time a different frequency is required.

By changing the two fixed resistors, R₂ and R₃ for a dual-ganged potentiometer and keeping the values of the capacitors the same, the frequency from the Astable Multivibrators output can be more easily “tuned” to give a particular frequency value or to compensate for the tolerances of the components used.

For example, selecting a capacitor value of 10nF from the table above. By using a 100kΩ’s potentiometer for our resistance, we would get an output frequency that can be fully adjusted from slightly above 71.4kHz down to 714Hz, some 3 decades of frequency range. Likewise a capacitor value of 47nF would give a frequency range from 152Hz to well over 15kHz.

Astable Multivibrator Example No2

An Astable Multivibrator circuit is constructed using two timing capacitors of equal value of 3.3uF and two base resistors of value 10kΩ. Calculate the minimum and maximum frequencies of oscillation if a 100kΩ dual-gang potentiometer is connected in series with the two resistors.

With the potentiometer at 0%, the value of the base resistance is equal to 10kΩ.

with the potentiometer at 100%, the value of the base resistance is equal to 10kΩ + 100kΩ = 110kΩ.

Then the output frequency of oscillation for the astable multivibrator can be varied from between 2.0 and 22 Hertz.

When selecting both the resistance and capacitance values for reliable operation, the base resistors should have a value that allows the transistor to turn fully “ON” when the other transistor turns “OFF”. For example, consider the circuit above. When transistor TR₂ is fully “ON”, (saturation) nearly the same voltage is dropped across resistor R3 and resistor R4.

If the transistor being used has a current gain, β of 100 and the collector load resistor, R4 is equal to say 1kΩ the maximum base resistor value would therefore be 100kΩ. Any higher and the transistor may not turn fully “ON” resulting in the multivibrator giving erratic results or not oscillate at all. Likewise, if the value of the base resistor is too low the transistor may not switch “OFF” and the multivibrator would again not oscillate.

An output signal can be obtained from the collector terminal of either transistor in the Astable Multivibrators circuit with each output waveform being a mirror image of itself. We saw above that the leading edge of the output waveform is slightly rounded and not square due to the charging characteristics of the capacitor in the cross-coupled circuit.

But we can introduce another transistor into the circuit that will produce an almost perfectly square output pulse and which can also be used to switch higher current loads or low impedance loads such as LED’s or loudspeakers, etc without affecting the operation of the actual astable multivibrator. However, the down side to this is that the output waveform is not perfectly symmetrical as the additional transistor produces a very small delay. Consider the two circuits below.

Astable Multivibrators Driving Circuit

An output with a square leading edge is now produced from the third transistor, TR₃ connected to the emitter of transistor, TR₂. This third transistor switches “ON” and “OFF” in unison with transistor TR₂. We can use this additional transistor to switch Light Emitting Diodes, Relays or to produce a sound from a Sound Transducer such as a speaker or piezo sounder as shown above.

The load resistor, Rx needs to be suitably chosen to take into account the forward volt drops and to limit the maximum current to about 20mA for the LED circuit or to give a total load impedance of about 100Ω for the speaker circuit. The speaker can have any impedance less than 100Ω.

By connecting an additional transistor, TR₄ to the emitter circuit of the other transistor, TR₁ in a similar fashion we can produce an astable multivibrator circuit that will flash two sets of lights or LED’s from one to the other at a rate determined by the time constant of the RC timing network.

In the next tutorial about Waveforms and Signals, we will look at the different types of Astable Multivibrators that are used to produce a continuous output waveform. These circuits known as relaxation oscillators produce either a square or rectangular wave at their outputs for use in sequential circuits as either a clock pulse or timing signal. These types of circuits are called Waveform Generators.

examples

The Schmitt Trigger is a logic input type that provides hysteresis or two different threshold voltage levels for rising and falling edge. This is useful because it can avoid the errors when we have noisy input signals from which we want to get square wave signals.

So for example, if we have a noisy input signal like this, that is meant to have 2 pulses, a device that has only one set point, or threshold, could get incorrect input and it could register more than two pulses as shown in this illustration. And if we use the Schmitt Trigger for the same input signal we will get a correct input of two pulses because of the two different thresholds. So that’s the primal function of the Schmitt Trigger, to convert noisy square waves, sine waves or slow edges inputs into clean square waves.

Types of Schmitt Trigers

---

There are many logic ICs that have built-in Schmitt Triggers on their inputs, but also it can be built using transistors or easier using an Operational Amplifier, or comparator and just adding some resistors to it and a positive feedback.

Operational Amplifier based Schmitt Trigger

---

Here we have an op-amp which inverting input is connected to the ground or zero volts and the non-inverting input is connected to a voltage input, V_IN. So this is actually a comparator and compares the non-inverting input to the inverting input or in this case the input voltage V_IN to 0 V. So when the V_IN value is below 0 volts the output of the comparator will be the negative V_CC and if the input voltage is above 0 volts the output will be positive V_CC.

Now if we add a positive feedback by connecting the output voltage to the non-inverting input with a resistor between them and another resistor between the V_IN and the non-inverting input we will get the Schmitt Trigger. Now the output will switch from V_CC– to V_CC+ when the voltage at the A node will cross 0 volts.

That means that now by adjusting the values of the resistors we can set at what value of the V_IN input the switch will occur using the following equations. We get these equations with the following relationships. The current “i” through this line equals V_IN – V_A divided by R₁ as well as V_A – V_OUT divided by R₂. So if we replace the V_A with zero, as we need that value for the switch to occur, we will get that final equation. For example if the output is -12 volts and the V_IN input is negative and rises, the switch from -12 V to +12 V will occur at 6 volts according to the equation and the values of the resistors and vice versa when the V_IN input is high and declines the switch from +12 V to – 12V will occur at -6 volts.

Non-Symmetrical Schmitt Trigger

---

In order to get two different non-symmetrical thresholds, we can use this circuit of an inverting single powered Schmitt Trigger. Here the V_REF voltage is the same as the V_CC of the op-amp. Now because the V_IN input is connected to the inverting input of the op-amp when its values will reach the upper threshold, the output will switch off to 0 volts, and then when its values will decline to the lower threshold, the output will switch on to 5 volts.

Here’s an example of how we can calculate the thresholds. The V_REF and the V_CC will be 5 volts and the three resistors will be the same 10k ohms. So what we need to calculate now is the voltage at the A node. In the first case when the output is 0 V our circuit will look like this, a simple voltage divider and the value of the V_A will be 1.66 V. This means that the V_IN input needs to decline below that value in order the output to switch on to 5 volts. Now with this 5 volts at the output the circuit will look like this. The value of the V_A will be 3.33 V. This means that the V_IN input needs to rise above that value in order the output to switch off to 0 volts.

The Schmitt Trigger is a logic input type that provides hysteresis or two different threshold voltage levels for rising and falling edge. This is useful because it can avoid the errors when we have noisy input signals from which we want to get square wave signals. The Transistor Schmitt Triger circuit contains two transistors and five resistors. For better explanation I will assign values to the components, and later I will make demonstration and build this circuit on a protoboard to see how it really works.

We will start like this. Let’s suppose that the Vin input is 0 V. That means that transistor T1 is cut off and not conducting. On the other hand the Transistor T2 is conducting because we have a voltage of about 1.98 V at the B node as we can consider this part of the circuit as a voltage divider and calculate the voltage using this expressions.

So because the Transistor T2 is conducting the output voltage will be low and the voltage at the emitter will be about 0.7 V lower than the voltage at the base of the transistor, or that’s about 1.28 V.

The emitter of the transistor T1 is connected with the emitter of the transistor T2 so they are at the same voltage level of 1.28 V which means that the transistor T1 will turn on when the voltage Vin at its base will be 0.7 V above this value of 1.28 V, or about 1.98 V.

So as we increase the Vin input and we cross this value of 1.98 the transistor T1 will start conducting. This will cause the voltage at the base of the transistor T2 to drop and will cut the transistor off. As the transistor T2 is no longer conducting the output voltage will go high.

Next, the voltage Vin at the base of the transistor T1 will start declining and it will turn the transistor off when the base voltage will be 0.7 V above the voltage of its emitter. This will happen as the current in the emitter will decline to a point where the transistor will get into forward-active mode. In this mode the collector voltage will increase, which will also increase the voltage at the base of the transistor T2. This will cause small amount of current to flow through the transistor T2 which will further drop the voltage at the emitters and will cause the transistor T1 to turn off. In our case the Vin input needs to drop to about 1.3 V to turn off the transistor T1.

That’s it. Now the cycle repeats over and over again. So we got two thresholds, the high threshold at about 1.9 V and the low threshold at about 1.3 V.

we can volt at node A by use thevenin’s theorem if v_ref =5 and v_in=1.4 and h_fe=220

note:
in the previous circuit the current pass the transistor is constant current not affected by remaining of the circuit because that we not use the emitter resistor to calculate R_th